[PS] 핵심 정리
in PS
leetcode, programmers 를 풀면서 얻은 노하우를 정리합니다. cracking the coding interview 6/e 내용도 일부 포함되어 있습니다.
잡스킬
입력
import sys
input = sys.stdin.readline
str = input()
num = int(input())
flt = float(input())
str1, str2 = input().split()
num1, num2 = map(int, input().split())
최대값, 최소값
# 3.5 이상
max_ = float('inf')
min_ = float('-inf')
and, or 연산자 활용
# 하나라도 False 면, None
# 둘다 False 가 아니면, 뒤에 값에 의존
print(3 and 5) # 5
print(None and 5) # None
print(3 and None) # None
# 둘다 False 가 아니면, 앞의 값에 의존
print(3 or 5) # 3
print(None or 5) # 5
print(3 or None) # 3
자료구조
배열과 문자열
# 배열 초기화
arr_1d = [0] * 100
arr_2d = [[0] * 20 for _ range(10)] # 10X20
arr_3d = [[[0] * 30 for _ range(20)] for _ range(10)] # 10X20X30
arr_empty = [[] for _ in range(5)] # [[] [] [] [] []]
# zip 메서드를 이용해 2d 행렬 transpose
arr = [
[1,1,1],
[2,2,2],
[3,3,3]
]
arr_tr = list(map(list, zip(*arr))) # [[1,2,3], [1,2,3], [1,2,3]]
alpha = 'abcd'
digit = '123'
negative = '-1'
# 문자인지
alpha.isalpha() # True
# 숫자인지
digit.isdigit() # True
# 음수는 False
negative.isdigit()
# 문자 혹은 숫자인지
alpha.isalnum() # True
digit.isalnum() # True
# 아스키코드
to_ord = ord('A') # 65
to_chr = chr(65) # 'A'
# 2진법, 10진법
bin_val = bin(10) # '0b1010'
dec_val = int('1010', 2) # 10
# count
'hobby'.count('b') # 2
# find
'python is the best choice'.find('b') # 14, 없으면 -1
# join
','.join('abc') # 'a,b,c,d'
# upper
a = 'hi'
a.upper() # 'HI'
# strip
a = ' hi '
a.lstrip() # 'hi '
a.rstrip() # ' hi'
a.strip() # 'hi'
# replace
'Life is too short'.replace('Life', 'Your leg') # 'Your leg is too short'
# split
'Life is too short'.split() # ['Life', 'is', 'too', 'short']
'a:b:c:d'.split(':') # ['a', 'b', 'c', 'd']
# 숫자 자릿수 더하기
num=12345
digit_sum = sum(int(c) for c in str(num))
해시테이블
- 밸류 구조로 평균 O(1) 탐색이 가능하다. 파이썬에서는 딕셔너리를 쓰면 된다.
- 연결리스트와 해시 코드 함수를 가지고 구현할 수 있음
- 키의 해시코드 계산
- 해시코드를 이용해 배열의 인덱스 계산
- 해당 인덱스에 저장하되, 해시 충돌을 대비해 연결리스트 이용
- 일반적으로는 탐색 시간
O(1). 충돌이 자주 발생하는 경우, 탐색 시간 O(N) - 균형 이진 탐색 트리를 이용해서 구현할 수도 있음. 탐색 시간
O(logN)
관련 문제
hash_map = {}
# insert
hash_map['dog'] = 'doggy'
# find - O(1)
'cat' in hash_map.keys()
# 초기값 지정, 갯수 셀 때 유용
import collections
dic = collections.defaultdict(int) # 0으로 초기화
# collections.Counter 모듈로 갯수 세기
from collections import Counter
Counter('hello world') # Counter({'l': 3, 'o': 2, 'h': 1, 'e': 1, ' ': 1, 'w': 1, 'r': 1, 'd': 1})
Counter('hello world').most_common() # [('l', 3), ('o', 2), ('h', 1), ('e', 1), (' ', 1), ('w', 1), ('r', 1), ('d', 1)]
# 딕셔너리 정렬 혹은 최대/최소값
x = {'a':10, 'b':5, 'c':30}
sorted(x.items(), key=lambda x: x[1]) # value 로 정렬
max(x.items(), key=lambda x: x[1]) # value가 최대인 k,v 튜플 리턴
# 삭제
dic = {'a': 1, 'b': 2}
del dic['a']
print(dic) # {'b': 2}
연결리스트
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
- 노드 추가/삭제에 능숙해야 함
- 투 포인터 기법이 많이 활용됨(slow, fast)
- 한번에 두 칸씩 가는
fast포인터와 한 칸씩 가는slow포인터가 있을 때,fast포인터가 끝에 도달하면slow포인터는 가운데 지점에 있게 됨
- 한번에 두 칸씩 가는
- 많은 문제가 재귀식으로 풀림
관련 문제
스택/큐
from collections import deque
d = deque()
# 오른쪽에 삽입
d.append(2); d.append(3) # deque([2,3])
# 왼쪽에 삽입
d.appendleft(1) # deque([1,2,3])
# 오른쪽 요소 삭제
d.pop() # deque([1,2])
# 왼쪽 요소 삭제
d.popleft() # deque([2])
# 스택 탑 반환
d[-1]
# 길이 반환
len(d)
- 스택은 재귀 알고리즘을 사용할 때 유용. 혹은 재귀 알고리즘을 스택을 이용해 iterative 하게 구현할 수도 있음
- 큐는 너비 우선 탐색을 하거나 캐시를 구현하는 경우에 사용
관련 문제
트리
사이클이 없는 그래프. DAG의 한 종류
이진 트리 종류
- 이진 탐색 트리: 모든 왼쪽 자식들 <= 루트 < 모든 오른쪽 자식들. 중위 순회 시 정렬된 결과
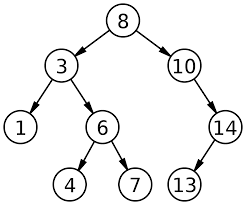
균형 트리: 왼쪽 오른쪽 부분 트리 높이가 완전히 같은 필요는 없지만, 탐색 시간이 O(logn) 에 근사
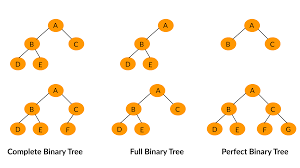
완전 이진 트리(Complete Binary Tree): 노드가 왼쪽에서 오른쪽으로 채워짐. 모든 트리가 꽉 차 있을 필요는 없음
전 이진 트리(Full Binary Tree): 모든 노드의 자식이 없거나, 정확히 두 개만 있는 경우
포화 이진 트리(Perfect Binary Tree): 전 이진 트리면서 완전 이진 트리. 모든 리프 노드가 같은 높이에 있고, 마지막 단계 노드의 개수가 최대
트리 순회
# 전위 순회: 항상 루트부터 방문
def preorder(root):
return [root.val] + preorder(root.left) + preorder(root.right) if root else []
# 중위 순회: BST 에서 항상 정렬된 결과
def inorder(root):
return inorder(root.left) + [root.val] + inorder(root.right) if root else []
# 후위 순회: 리프 노드부터 먼저 방문
def postorder(root):
return postorder(root.left) + postorder(root.right) + [root.val] if root else []
관련 문제
힙
완전 이진 트리이면서 원소가 정렬되어 있음
- 최소 힙: 루트 노드가 최소값이고, 각 원소는 항상 자식 원소들보다 작거나 같음
- 최대 힙: 루트 노드가 최대값이고, 각 원소는 항상 자식 원소들보다 크거나 같음
파이썬에서는 heapq 모듈을 쓰자. (최소힙)
import heapq
heap = []
# insert - log(N)
heapq.heappush(heap, 4)
heapq.heappush(heap, 1)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)
print(heapq) # [1, 3, 7, 4]
# delete - log(N)
print(heapq.heappop(heap)) # 1
print(heap) # [3, 4, 7]
# 최소값 출력
print(heap[0]) # 4
# 기존 리스트를 힙으로 - O(N)
heap = [4, 1, 7, 3, 8, 5]
heapq.heapify(heap)
- 응용 k번째 최소값/최대값
# 참고: https://www.daleseo.com/python-heapq/
def kth_smallest(nums, k):
heap = []
for num in nums:
heapq.heappush(heap, num)
kth_min = None
for _ in range(k):
kth_min = heapq.heappop(heap)
return kth_min
print(kth_smallest([4, 1, 7, 3, 8, 5], 3)) # 4
- 응용 힙 정렬
# 참고: https://www.daleseo.com/python-heapq/
def heap_sort(nums):
heap = []
for num in nums:
heapq.heappush(heap, num)
sorted_nums = []
while heap:
sorted_nums.append(heapq.heappop(heap))
return sorted_nums
print(heap_sort([4, 1, 7, 3, 8, 5]))
트라이
- 접두사 트리(prefix tree)
- n차 트리 변종으로 각 노드에 문자를 저장하는 자료구조
- 널 노드라고 불리우는 ‘* 노드’는 단어의 끝을 나타냄
- 각 노드는
알파벳 크기 + 1개까지 자식을 갖고 있을 수 있음(* 노드포함) - 길이 K인 문자열이 주어졌을 때 O(K) 시간에 해당 문자열이 유효한 접두사인지 확인 가능
그래프
n,m,v = map(int, input().split())
visited = [False] * (n+1)
edges = [[] for _ in range(n+1)]
for _ in range(m):
a,b = map(int, input().split())
edges[a].append(b)
edges[b].append(a)
DFS
- 재귀함수를 이용하자(스택)
- 모든 노드를 방문하고자할 때 주로 사용
def dfs(x):
visited[x] = True
print(x, end=' ')
for nbr in nbrs[x]:
if not visited[nbr]:
dfs(nbr)
dfs(v)
BFS
- 큐를 이용하자
- 최단 경로 찾을 때 주로 사용
- 양 방향 탐색에서도 사용(출발지, 도착지 각각에서 BFS 수행): O(K**(d/2))
deq = deque()
deq.append(v)
visited[v] = True
while len(deq):
cur = deq.popleft()
print(cur, end=' ')
for nbr in nbrs[cur]:
if not visited[nbr]:
visited[nbr] = True
deq.append(nbr)
관련 문제
알고리즘
정렬
- 파이썬
sort()함수는 stable 함 key=파라미터를 통해 정렬 기준을 정할 수 있음reverse=True를 통해 내림차순으로 바꿀 수 있음
dictionary 정렬
x = {1: 2, 3: 4, 4: 3, 2: 1, 0: 0}
sorted_x = {k: v for k, v in sorted(x.items(), key=lambda item: item[1])}
{0: 0, 2: 1, 1: 2, 4: 3, 3: 4}
- 머지 소트
def merge_sort(arr):
def merge(left, right):
result = []
while len(left) and len(right):
if left[0] <= right[0]:
result.append(left[0])
left = left[1:]
else:
result.append(right[0])
right = right[1:]
while len(left):
result.append(left[0])
left = left[1:]
while len(right):
result.append(right[0])
right = right[1:]
return result
if len(arr) <= 1:
return arr
mid = len(arr) // 2
leftList = merge_sort(arr[:mid])
rightList = merge_sort(arr[mid:])
return merge(leftList, rightList)
- 퀵 소트
- 평균 O(n logn) 최악 O(n^2). 메모리: O(logn)
# 쉬운 버전
def quick_sort(arr):
n = len(arr)
if n <= 1:
return arr
else:
pivot = arr[0]
left = [ element for element in arr[1:] if element <= pivot ]
right = [ element for element in arr[1:] if element > pivot ]
return quick_sort(left) + [pivot] + quick_sort(right)
# 최적화 버전 (in-place)
def quick_sort(arr):
def sort(left, right):
if left >= right:
return
mid = partition(left, right)
sort(left, mid-1)
sort(mid, right)
def partition(left, right):
pivot = arr[(left+right)//2]
while left <= right:
while arr[left] < pivot:
left += 1
while arr[right] > pivot:
right -= 1
if left <= right:
arr[left], arr[right] = arr[right], arr[left]
left, right = left+1, right-1
return left
sort(0, len(arr)-1)
완전 탐색
- BFS/DFS 로 대부분 품
- 순열 혹은 조합이 필요한 경우에는
permutations혹은combinations사용
from itertools import permutations, combinations
a = [1,2,3]
print(list(permutations(a,2))) // aP2
print(list(combinations(a,2))) // aC2
이분 탐색
- 어떤 기준을 가지고 이분할 수 있는 경우
def binary_search(arr, x):
l,r = 0,len(arr)-1
while l <= r:
mid = (l+r)//2
if arr[mid] == x:
return mid
if arr[mid] < x:
l = mid+1
elif arr[mid] > x:
r = mid-1
return -1
bisect모듈에서bisect_left()혹은bisect_right()메소드를 사용해도 됨
arr = [1,2,3,4,5]
bisect_left(arr, 0) # 5
bisect_left(arr, 3) # 2
bisect_right(arr, 3) # 3
시뮬레이션
빡구현은 그냥 빡구현이야
다이나믹 프로그래밍
- 이전 결과를 활용해서 현재 결과를 구할 수 있는 경우
- 처음 몇 단계 직접 계산하면서 패턴 파악
- 점화식 구하는 것이 핵심
